Sudoku game play is the same as all other difficulties on 24/7 Sudoku. Place the numbers 1 through 9 into each row, 3x3 box, and column only once. Complete the entire sudoku puzzle with the correct numbers to win. Hard Sudoku differs from easier difficulties, in that there can be multiple spaces where the answer is not immediately obvious. Sudoku Coach is useful to overcome a difficult step for a grid (when you find yourself a little stuck), but also to train and learn the techniques of sudoku experts, applying them to the real case which we are confronted. You can download the demo version, fully functional but time limited. We hope you have as much fun using it as we to conceive. The goal of Sudoku is to fill a 9×9 grid with numbers so that each row, column and 3×3 section contain all of the digits between 1 and 9. As a logic puzzle, Sudoku is also an excellent brain game. If you play Sudoku daily, you will soon start to see improvements in your concentration and overall brain power.
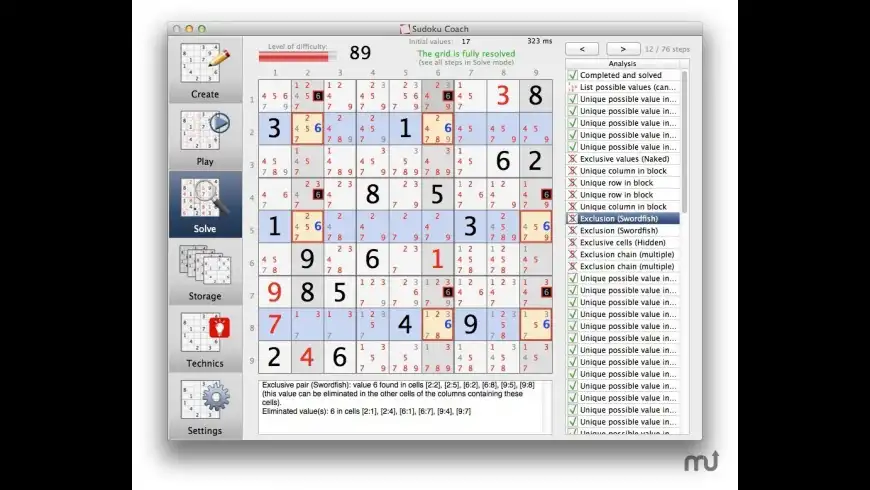
Let us define a Strong Link as the relationship that exists between two Cells in a region (Row, Column or Square) when these two Cells are the only Cells in that region that contain a particular candidate: if the candidate is not the solution for the first Cell, it must be the solution for the second Cell, and vice-versa.
If we consider a 'Bi-Value' Cell, asserting that one of its candidates is not the solution implies that its other candidate must be the solution. Hence there also exists a Strong Link between the two candidates of a 'Bi-Value' Cell.
- Sudoku is a fun puzzle game once you get the hang of it. At the same time, learning to play Sudoku can be a bit intimidating for beginners. So, if you are a complete beginner, here are a few Sudoku tips that you can use to improve your Sudoku skills. Tip 1: Look for rows, columns of 3×3 sections that contain 5 or more numbers.
- Sudoku strategies explained with graphics. If a 'Three-Value' Cell can 'see' (a Cell 'sees' another Cell if both Cells belong to the same region) two other 'Bi-Value' Cells that contain different combinations of the candidates of the first Cell, then the candidate common to the two 'Bi-Value' Cells can not be the solution in any Cell that 'sees' these three Cells.
If two Strong Links share a common Cell, we can form a Chain of three Cells with the common Cell in the middle. If we assume that the candidate in the Cell at one end of the Chain is not the solution for that Cell, then it must be the solution for the next Cell in the Chain because of the definition of a Strong Link. This, in turn and for the same reason, implies that the candidate can not be the solution for the third Cell in the Chain.
Conversely if we assume that the candidate in the Cell at one end of the Chain is the solution for that Cell, then it can not be the solution for the middle Cell and it must be the solution in the other end Cell of the Chain.
If we consider a longer Chain exclusively made of Strong Links, the successive Nodes alternate from one state to the other.
Sudoku Coaching
This strategy analyzes such chains and uses colors to display these states. Because there are only two possible states, all candidates with the same color simultaneously must be the solution or can not be the solution.
Sudoku Coach
3D MEDUSA (SAME COLOR TWICE IN A CELL) : We know that one of the two colors is the solution. As two candidates can not simultaneously be the solution for a Cell, the corresponding color can not be the solution; all candidates with this color can be eliminated. The other color is the solution.
In the example, starting with coloring candidate 3 in J3 leads to candidates 1 and 3 in G3 being both colored in yellow. As two different candidates can not be the solution in a particular Cell, the yellow chain can not identify the solution. The candidates colored in green are the solution and all candidates colored in yellow can be eliminated.
3D MEDUSA (TWICE IN A UNIT) : if two Nodes in the Chain belong to the same region (Row, Column or Square) and if they have the same color for the same candidate, then this color can not be the solution because a candidate can not be the solution for two cells in the same region; all candidates with this color can be eliminated. Hence the other color is the solution.
In the example, candidate 3 is colored in yellow in A9 and in H9. If the yellow color identified the solution, then candidate 3 would be the solution for two Cells in Column '9' which is impossible. Hence the green color identifies the solution and all candidates colored in yellow can be eliminated.
However this is a theoritical case. The chain is built using iterations. The iteration 'coloring' the 'second node' in the same unit is preceded by the iteration that has colored the linked node with the other color. Which means that during this preceding iteration, the 'second node' already saw two candidates with differing colors (see below). In the example, before being colored in yellow, candidate 3 in H9 sees a yellow candidate 3 in A9 and a green candidate 3 in H4. Hence rule '3D MEDUSA (SEES TWO DIFFERENT COLORS)' would have been applied before coloring candidate 3 in H9 in yellow.
3D MEDUSA (TWO COLORS IN A CELL) : One of the two colors is the solution. If there are two candidates with different colors in a Cell, one of them must be the solution for that Cell. Hence all other candidates can be eliminated from the Cell.
In the example G9 must have either candidate 1, or candidate 5, as solution. The other candidates in this Cell can not be the solution.
3D MEDUSA (SEES TWO DIFFERENT COLORS) : Either one, or the other, color is the solution. If an uncolored candidate can 'see' (a Candidate 'sees' another Candidate if both Candidates belong to the same region) two candidates of different colors, then it is eliminated by one of them (we do not know yet by which one).

In the example, candidate 7 in C9 sees candidates 7 of different colors in A8 and in C1. As candidate 7 must be the solution in one of these cells, it can not be the solution in C9.
3D MEDUSA (UNIT-CELL ELIMINATION) : Either one, or the other, color is the solution. If an uncolored candidate can 'see' a colored candidate with the same value and another candidate in its own Cell with the other color, then it can not be the solution and it can be eliminated.
In the example either candidate 9 is the solution in C9, or candidate 1 is the solution in F9. As candidate 1 in C9 sees both candidates, it can not be the solution in C9.
Sudoku Coach
3D MEDUSA (EMPTYING A CELL) : If a particular uncolored Cell can 'see' Cells that each contain one of the candidates of the uncolored Cell and if all these candidates have the same color, then this color can not be the solution. Indeed, if it were the solution, it would eliminate all candidates from the particular Cell, which is not possible.

In the example if candidate 2 were the solution in B4 and candidate 9 the solution in E7, then all possible candidates would be eliminated in E4.
You can practice this strategy by installing the SudokuCoach application on your Android™ device.

